Расчёт индуктивности многопроволочных кабельных жил в программной среде ELCUT

Ранее^1,2) были рассчитаны погонные ёмкости триад и витых пар простейших конструкций с учётом эффектов скрутки как однопроволочных жил в сердечниках так и проволок в многопроволочных жилах. Сформулированная же в названии статьи задача несколько сложнее. Это связано с существенной разницей в протекании электрических и электромагнитных процессов в рассматриваемых объектах.

И потому уместно обсудить этот вопрос несколько подробнее.

Ёмкость C – это коэффициент пропорциональности между потенциалом U проводника и его зарядом Q: Q = CU.

Расчёт С для проводников кабелей существенно облегчен рядом обстоятельств.

Во-первых, электрическое поле в проводники практически не проникает, так как заряд электризованных металлов сосредоточен в приповерхностном слое толщиной порядка радиуса дебаевской экранировки

εε₀ (U/en)^1/2 ~ 10^-10 м, где n ~10²⁸ ...10²⁹ м^-3 – концентрация носителей заряда в металлах, ε – диэлектрическая проницаемость. Этот радиус порядка межатомного расстояний в решётке металла, так что их объёмы практически «выключены» из электростатических процессов. Это существенно облегчает процедуру вычисления различных контурных и поверхностных интегралов.

Во-вторых, время проникновения электрического поля в металлы исчезающе мало: оно порядка εε₀ /σ ~ 10^-18с – максвелловского времени релаксации.

В-третьих, за время Ø/V ~10^-11 с (~100 ГГц; V = 1 мм – диаметр проводника, V ~ 2 10⁸ м/с – скорость распространения электромагнитного поля вдоль кабеля) происходит выравнивание U на поверхности провода. Это намного меньше характерной длительности сигналов (иногда это обстоятельство формулируют иначе: длина волны много больше поперечного размера линии связи). Кроме того, ёмкости они не зависят от частоты (если нет частотной зависимости ε).

Так что с помощью указанного выше общепринятого выражения можно практически однозначно определить величины ёмкостных параметров кабельной продукции.

Чего нельзя сказать про погонные индуктивные параметры L проводников, если традиционно понимать их как коэффициенты пропорциональности связывающие поток магнитной индукции Ф вокруг проводника и его ток J:

Ф = LJ       (1)

Или иным математически эквивалентным способом (например, через эдс электромагнитной индукции, энергию магнитного поля: см. ниже). Это связано с тем, что, в отличие от электрического, магнитное поле в проводники проникает, причём на частотах

ω < 1/[زµ₀σ] ~ 10⁴ 1/c почти полностью (µ₀ = 4π 10^-7 Гн/м, для меди σ = 5.98 10⁷ Сим/м).

Причём из-за скин-эффекта и эффекта близости токи и магнитные поля распределены по сечению проводников неоднородно. Кроме того, время диффузии магнитного поля в проводник 1/ω ~ 10^-4 с соизмеримо со временами сигнальных процессов.

По всем этим причинам выражения типа (1) однозначно определяют индуктивный параметр L только для проводников и токов с особо высокой симметрией (плоской или коаксиальной). И не работают в применении к кабельной продукции с произвольной формой поперечного сечения проводников. В том числе и для рассмотренных в данной работе многопроволочных жил. И потому для однозначного определения индуктивности этих проводников необходимы дополнительные соображения.

Цель настоящей работы – такое уточнение понятия индуктивности, которое можно было бы использовать для получения однозначных расчётных величин индуктивных параметров. Имея в виду их связь:
- с геометрией проводов и свойствами их материалов с одной стороны;
- со скоростью распространения электромагнитного поля, волновым сопротивлением и другими наблюдаемыми величинами – с другой стороны;
- а также искробезопасностью и другими эксплуатационными свойствами кабельной продукции.

Решение поставленной задачи обусловило следующий план статьи.

Сначала произведено уточнение подлежащего расчётам индуктивного параметра линий. Потом в среде ELCUT произведено вычисление индуктивности в коаксиальных линиях - простейшем объекте с однозначно определённой величиной индуктивного параметра (как будет показано ниже – это индуктивный инвариант). Главным образом для того, чтобы сравнить результат с точно известным³⁾.

Затем произведен расчёт индуктивных параметров многопроволочной жилы, как примера проводника со сложной формой поперечного сечения. А также для проверки с помощью ELCUT наличия у проводников данного типа индуктивного инварианта.

В приложениях приведены некоторые необходимые для применения ELCUT математические рассуждения и доказательство теоремы об «индуктивном инварианте».

Для наглядности и упрощения рассуждений, в данной работе мы рассматриваем объекты, конструкция которых не усложнена скруткой сердечников кабелей и жил в них. Оставив эти вопросы для отдельного обсуждения.

Традиционные определения индуктивности

Существуют разные по физическому смыслу определения индуктивности L (контура, катушки и тд). Кроме определения L в (1), другие связывают этот параметр с:
- эдс Э электромагнитной индукции Э = – L dJ/dt;
- энергией W этого магнитного поля W = L J2/2;
- мнимой частью потока П вектора [E H*] L = Im (П/ω);

Здесь [E H*] – вектор Умова-Пойтинга, П = – ∫ [E H*] dS, dS – элемент поверхности⁴⁾, Н* – комплексно-сопряжённая амплитуда магнитного поля.

Все эти L однозначно определены и математически идентичны, если:
- провода бесконечно тонкие;
- среда, где «живет» магнитное поле, не поглощающая;
- контуры с током точечные.

Из последнего, помимо прочего, следует, что индуктивность – сугубо сосредоточенный параметр.

В линиях связи, силовых кабелях и вообще в системах с распределёнными параметрами не выполняется ни одно из перечисленных условий. Поэтому вводят понятие погонных параметров (их ещё называют первичными): ёмкости С (например, нФ/км) и индуктивности L (мГн/км). Однако в учебной и другой литературе в их определении есть разнобой. И потому уточним, о чём будем говорить.

Индуктивные параметры длинных линий

Рис.1 Схема построения телеграфных уравнений для коаксиального кабеля.

Рассмотрим отрезок z, z +dz двухпроводной линии (рис.1) . Пусть это – коаксиальный кабель c радиусом экрана b и радиусом жилы a (это упростит рассуждения, без умаления их общности). В жиле течёт ток J, распределённый в ней с плотностью σж(r,φ). В экране – противоположный ток с плотностью σэ(r,φ). Если проводимость σ проводников конечна, то на их поверхности есть продольное электрическое поле

Еж = δж/σж и Еэ = δэ/σэ

Здесь δж = δж (а,φ) и δэ = δэ(b,φ) – плотность тока на поверхности жилы и экрана, а σж(а,φ) и σэ(b,φ) – электропроводность. Последняя может меняться по глубине (например, поверхность медных жил может быть лужёной или серебрёной).

В приближении телеграфных уравнений в линии идёт только потенциальная Т-волна. По этой причине для эдс Э индукции по указанному на рисунке контуру (пунктир) можно записать:

– (d/dt) ∫В(r) drdz = Э = – U(z) + Еэdz + U(z + dz) + Ежdz

где: Ф = ∫В(r) drdz – поток магнитной индукции сквозь контур. Отсюда получаем первое телеграфное уравнение (в алгебраической форме):

– dU/dz = jωL* J      (2)

где: L*= L + R*/ jω – обобщённая погонная индуктивность (далее термин погонный опускаем). В коаксиальной геометрии В(r) = J µ₀/2πr, и интеграл легко вычислить:

L = ∫В(r)dr /J = (µ₀/2π) ln(b/a);      (3)

R* = [δэ/σэ + δж/σж] / J = Rэ* + Rж*.

Параметр R* обычно называют сопротивлением, так как предел ω -> 0, R* -> R/Д, где: R – суммарное омическое сопротивление постоянному току проводников линии. Д – её длина. А L называют (межпроводной) индуктивностью, по аналогии со сосредоточенной. Хотя по смыслу это – принципиально разные понятия.

Дело в том, что сосредоточенная индуктивность L – это вполне наблюдаемая величина, так как, к примеру, в (1) величины Э и dJ/dt могут быть измерены без разрушения L. Чего нельзя сказать о величинах dU/dz и/или J (z) в (2): их не измерить без разрушения параметров линии. И потому погонная индуктивность L – не наблюдаемый параметр. Равно как и другие первичные параметры длинных линий: межпроводная ёмкость С, сопротивление R и проводимость G = Go + ωC tgδ, где Go – проводимость изолятора на постоянном токе, tgδ – тангенс диэлектрических потерь.

Связь индуктивности с волновыми свойствами и искробезопасностью линий связи

Первичные параметры линий тесно связаны с наблюдаемыми вторичными параметрами: волновым импедансом Z и волновым числом k. А через них – с токами, напряжениями и частотами. Воспользуемся этой связью в телеграфной теории:

Z = [jωL*/(jωC + G)]^1/2 ;

k = [jωL* (jωC + G)]^1/2

Если пренебречь потерями, то

Z = [(L+Lэ+Lж) /C ]^1/2 ;

k = jω [(L+Lэ+Lж) C]^1/2 = j ω/V = j 2π/λ

где: L, Lэ, Lж определены ниже, V = 1/ [(L + Lэ+ Lж) C]^1/2 – скорость волны, λ – её длина.

Величина Z = ± U/J определяет связь между амплитудами волн токов и напряжений в линии связи (знак плюс – для волны вдоль z, минус – встречной). И является важнейшей в физике и технике передачи информации.

Она же тесно связана и с искроопасностью кабеля. Пусть, к примеру, на участке Д изоляции провода накопился статический заряд Q, который поднял потенциал этого участка до пробивного уровня U = Q/CД (рис. 2). Тогда в обе стороны от места пробоя полетят волны обнуления потенциала, сопровождаемые скачками разрядного тока J ~ U/Z . Общая длительность такого пробоя невелика ~ Д/2V ~ 10^-8 с. К тому же мощность разряда ~UJ ~U2/Z ограничивается сопротивлением Z. И с этой точки зрения его надо увеличивать. То есть увеличивать L + Lэ + Lж и снижать С. Помимо прочего, это хорошо и по той причине, что при этом снижается и освобождаемая в пробое электрическая энергия ~ Д С U²/2.

Но не всё так просто. Пусть, к примеру, произошёл обрыв в проводе кабеля с Z = 100 Ом и постоянным током J = 10 А (рис. 2 внизу) . Тогда от этого места полетят волны обнуления тока, сопровождаемые скачком напряжения U ~ J Z ~ 1000 В с разными знаками на гранях обрыва. Это явление аналогично экстраэдс индукции ~ 2000 В при обрыве цепей с током, если в в них есть катушки индуктивности. В линиях экстраэдс действует в течение ~10^-5...10^-6 с – времени, пока волны проходят по линии взад-вперёд и её магнитная энергия рассеивается на концевых нагрузках. Но это в лучшем случае.

Рис.2 «Пробивные» волны в бесконечной длинной линии (жирные горизонтали). Вверху – при пробое изоляции на участке Д накопления статических зарядов. Показаны две расходящиеся волны обнуления статического потенциала U , сопровождаемые волнами разрядного тока J = U/Z . Внизу – аналогичные волны, возникающие при обрыве хотя бы одного проводника с током: волны обнуления тока, сопровождаемые скачком напряжения (до момента возможного пробоя: тогда от точки обрыва в обе стороны полетят волны обнуления потенциала и скачки тока).

В худшем в месте обрыва происходит пробой, и здесь может освободиться почти вся магнитная энергия. И потому для взрывоопасных смесей, сквозь которые проходят некоторые виды кабелей, «индуктивный запал» может оказаться опаснее ёмкостного. В этом случае полезнее как раз уменьшать волновое сопротивление.

В целом может оказаться так, что для коротких линий необходимо подбирать кабели с повышенным Z, а для длинных – наоборот. Или вообще собирать линии связи из кусков с разными Z. Для обеспечения минимальной искроопасности.

Таким образом, как с точки зрения передачи сигналов, так и с точки зрения безопасности, целесообразно рассматривать параметры линии, связанные именно с волновыми свойствами кабелей, как показано в предыдущем разделе.

Вычисляемые компоненты индуктивности

Как видно из (2), обобщённая индуктивность содержит ряд слагаемых:

L* = L + Zэ + Zж = L + Lэ + Rэ/ jω + Lж + Rж/ jω     (4)

Которые можно интерпретировать как вклад от межпроводниковой индуктивности L и реактивных составляющих импедансов обоих проводников:

Zэ = Rэ + jω Lэ; Zж = Rж + jω Lж

где, по определению:

Rэ = Re(Zэ); Lэ = Im(Zэ)/ω

Rж = Re(Zж); Lж = Im(Zж)/ω

или

Lэ = Im(δэ) / (J σэ ω); Rэ = Re(δэ) / (J σэ)

Lж = Im(δж) / (J σж ω); Rж = Re(δж) / (J σж)         (5)

Рис.3 К определению величин, необходимых для расчёта индуктивных параметров двухпроводных линий. И доказательства теоремы об индуктивном инварианте.

Здесь и далее мы рассматриваем проводники произвольной формы и симметрии (то есть не обязательно коаксиальной). По этой причине на рис. 3 заменим индексы ж и э числами 1 и 2. Этот рисунок поясняет процедуру вычисления индуктивных параметров, зависящих от выбора контура (поверхности) интегрирования S. Плотности тока проводников δ вычисляем вдоль линиий A₁ и A₂ касания поверхности S, «натянутой» между проводниками, сквозь которую вычисляем поток Ф = ∫ ВdS в выражении (3). Отметим, что в двумерном случае этот интеграл равен разности вектор-потенциалов линий A₂ и A₁. Поэтому

L = (А₂ – А₁) /J     (6)

Это резко облегчает процедуру расчётов в ELCUT, так как он решает задачу именно для вектор-потенциала А(r,φ).

Так как в проводниках и на их поверхности фазы и амплитуды А(r,φ), δж(r,φ) и δэ(r,φ), вообще говоря, зависят от координат, то индуктивные параметры проводников L, Lэ, Rэ, Lж, Rж не определены однозначно. И, как указано выше, чтобы получить для них определённые величины, нужны дополнительные соображения. Скажем, искробезопасности и/или величины волнового сопротивления линии. Тогда в качестве индуктивности целесообразно использовать максимум суммы L + Lэ + Lж. Тем паче, она – инвариант, то есть определена однозначно (см. Приложение). Проверим всё это с помощью ELCUT, для чего решим ряд простых задач.

Индуктивность однопроволочной жилы и прямой пары

Первая из них – индуктивность однопроволочной медной жилы радиуса а = 0.5 мм в коаксиальном сверхпроводящем экране (Lэ = 0; Rэ = 0) с радиусом b = 1.6 мм . Её межпроводниковая индуктивность L точно известна (для µ = 1):

L = µ µ₀ / 2π ln(b/a) = 0.232630 нФ/км

Известны также и параметры провода:

Lж = µ₀ / 2π aq [ber ber’ + bei bei’] / D;

Rж = aq / 2 [ber bei’ – ber’ bei] / D      (6)

где: q = (ω σ µ₀)^1/2, D = ber’² + bei’², ber(qa), bei(qa) – функции Томсона (Кельвина), штрихи – их производные.

Задача эта облегчается тем, что в осесимметричном случае А(r,φ) от угла не зависит и потому все указанные в (5) параметры определены однозначно.

Рис.4 Геометрическая модель расчета магнитного поля коаксиальной структуры (верх) и карта магнитного поля (черные кривые – силовые линии) и цветная - плотности тока в жиле линии (тёмно синий цвет – ток = 0) для разных частот.

Проверим это с помощью ELCUT, для чего построим геометрическую модель для коаксиального кабеля (рис.4). Модель представляет собой узкий сектор (100), на лучах которого определены граничные условия Нt = 0, а на внешней дуге – нуль вектор-потенциала А = 0 (приближение - сверхпроводящий экран). Медный жила оборудована вспомогательным ребром (радиус 0.45 мм) для увеличения густоты сетки конечных элементов (всего 251 узлов) в области скин-эффекта. Внизу на рис.4 представлена карта магнитного поля (черные линии) и плотности тока (цвет) при разных частотах. Видно, как по мере увеличения частоты магнитное поле выталкивается из проводника, а электрический ток прижимается к его поверхности (синий цвет – минимальный ток, теплые тона – максимальный). Это и есть скин-эффект.

В таблице приведены значения токов в центре провода δж(0) и δж(а) – на поверхности медного блока (красная точка). Вместе с параметрами L на разных частотах: L = А(а) / J, а также Lж и Rж. Справа от них – ошибки относительно расчётов по формулам (6).

Из таблицы видно, как с увеличением частоты падает амплитуда тока в центре провода, меняя при этом знак, и растёт ток на поверхности.

ELCUT с высокой степенью точности подтверждает, что в коаксиальных структурах параметр L не зависит от частоты (то есть определён однозначно). На частотах выше 1 МГц быстро растут ошибки вычислений в ELCUT параметров Rж и, особенно, Lж. Это, видимо, связано с развитием скин-эффекта, который заставляет увеличивать густоту сетки в приповерхностных слоях проводника. Но доступная версия ELCUT (255 узлов) не позволяет установить этот факт с надлежащей достоверностью. Тем не менее, даже в этой версии погрешность Rж относительно величины ωL не превышает 0.05% (в среднем 0.04%), а Lж 0.2% (0.12%). Во всём практически интересном диапазоне частот от 100Гц до 1000 МГЦ.

Для справок в таблице приведены значения глубины проникания (диффузии) магнитного поля в медь. Например, на частоте 1 МГц поле проникает в проводник на глубину ~0,2 мм. В этом же слое в основном текут токи. Что и приводит к росту на полпорядка сопротивления провода Rж и такому же падению его индуктивности Lж. На рис.5 синие точки – расчёт Rж и Lж в ELCUT, а кривые – точное решение (6). Совпадение впечатляет. Особенно, если учесть, что ELCUT не знает о существовании функций Бесселя, Томсона, Макдональда ... Светлые точки на рисунке – кривая для семипроволочной жилы (см. ниже).

Рис.5 Зависимость от частоты сопротивления жилы Rж (верхний график) и его индуктивности Lж (нижний). Синие точки - расчёт ELCUT, кривые – точное решение (см. текст). Светлые точки – для семипроволочной жилы.

Так как конформные отображения не меняют вид уравнения Лапласа ΔА = 0, индуктивность L коаксиального кабеля совпадает с аналогичным параметром всех его конформных отображений. В том числе симметричной прямой пары с соотношением

b’/a’ = (b/a +1) / [2(b/a)1/2]

(для рассматриваемого кабеля b’/a’ = 1.173936).

С другими индуктивными параметрами ситуация посложнее, так как для их вычислений необходимо решать уравнения Пуассона ΔА = – µµ₀δ, а конформные отображения, вообще говоря, меняют его вид, что исключает возможность прямого применения ELCUT. Задача, однако, облегчается тем обстоятельством, что дробно-линейное отображение практически не меняет вид и этого уравнения (см. Приложение). По этой причине результаты, полученные для коаксиальной структуры, полностью отображают свойства конформной ей пары.

Кроме того, в рассмотренной выше задаче экран был сверхпроводящим (Lэ = 0; Rэ = 0). А в симметричной паре он медный, и его роль можно учесть просто удвоением величин Rж и Lж, так как Rэ = Rж и Lэ = Lж. Полученные в данном разделе результаты могут быть применены и для несимметричных пар, то есть с разным диаметром и/или металлом жил. Для чего требуется лишь небольшое усложнение методики расчёта.

Индуктивность многопроволочной жилы

Рассмотрим коаксиальный кабель с жилой из семи проволок и сверхпроводящим экраном. Пусть площадь меди в жиле такое же, как рассмотренном выше примере (Ø = 1 мм, 0.785398 мм²) . Тогда диаметр проволоки 0.377964 мм, «большой» диаметр жилы 1.133893 мм, «малый» 1.032618 мм. А радиус экрана b = 1.814229 мм.

У конструкции есть ось симметрии шестого порядка и 12 плоскостей симметрии, поэтому расчёты производим в секторе 360/12 = 30⁰. На рис.6 представлен фрагмент геометрической модели с указанием характерных рёбер и точек (красные), для которых вычисляли вектор-потенциал, плотность тока и поток магнитной индукции. А также карты магнитного поля и токов для разных частот (рис.6). Видно, как семипроволочная жила выталкивает из своего объёма магнитное поле, а её ток прижимается к вершине внешней проволоки.

Рис.6 Геометрическая модель и карта магнитных полей (черные кривые) и плотности токов (синий цвет – ток = 0) для семипроволочной жилы, размещённой коаксиально относительно сверхпроводящего экрана для разных частот. Видно, как по мере увеличения частоты ток жилы оттесняется к её поверхности, а магнитное поле выталкивается из жилы. Красные линии на геометрической модели – контуры интегрирования для вычисления максимальной (контур К) и минимальной (В) величины межпроводниковой индуктивности L.

Синим пунктиром на карте 1 МГц обозначен радиус однопроволочной жилы (Ø = 1.0656 мм), которая имеет тот же индуктивный инвариант L + Lж, что и семипроволочная (см ниже). Частотный ход сопротивления многопроволочной жилы подобен однопроволочной того же сечения, причём на низких частотах они просто совпадают (рис. 5) . На высоких частотах сопротивление многопроволочной жилы заметно больше, так как работает только часть её поверхности.

Но намного интереснее частотный ход индуктивного параметра L, отображённый на рис. 7. Как указано выше, здесь именно тот случай, когда межпроводная индуктивность зависит от выбора контура, а параметр Lж – от точки на поверхности жилы. Для наглядности через расчётные точки ELCUT проведены кривые.

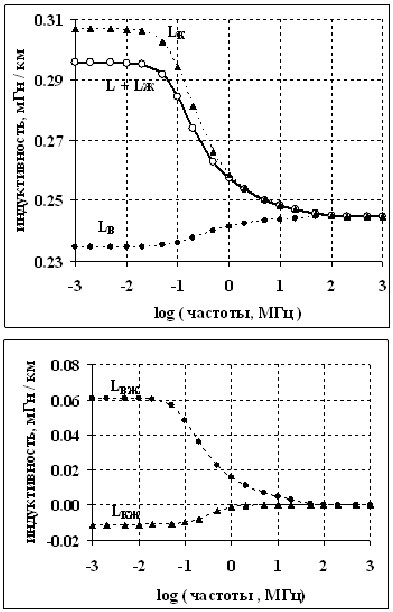
Рис.7 Частотная зависимость индуктивных параметров семипроволочной жилы, вычисленных для разных контуров и индуктивного инварианта L + Lж (см. текст).

Действительно, как видно из рисунка, индуктивность LK, вычисленная по контуру К (верхняя красная линия геометрической модели) заметно больше, чем LB, вычисленная по контуру В (нижняя линия). На частотах больше ~1 МГц, то есть по мере «отключения» проводника, это различие сходит на нет. И такое поведение понятно. Как видно из картины полей, на низких частотах магнитное поле проходит сквозь металл и поток магнитной индукции через контур К, больше. На высоких частотах поле выталкивается из проволок, и различие стирается.

Как видно из рис.7, индуктивный параметр LКЖ отрицательный. То есть металл в заглублении поверхности работает как бы «против» общей индуктивности. Аналогично встречно включённой обмотке трансформатора. Но самая интересная особенность этих расчётов ELCUT в том, что на всех частотах с погрешностью < 0.002% соблюдается равенство

L_K + L_КЖ = L_K + L_ВЖ

На рис. 7 вверху обе эти суммы показаны единой кривой L + Lж. Это и есть индуктивный инвариант. Так что ELCUT подтверждает справедливость упомянутой выше теоремы о существовании такого инварианта. Отметим попутно, что с погрешностью не больше 0.3% кривая L + Lж с совпадает с таковой для однопроволочной жилы с Ø = 1.0656 мм. Что тоже косвенно в пользу индуктивного инварианта: если у жил с произвольной формой поверхности есть таковой инвариант, то всегда можно подобрать круглый провод с таким же инвариантом и, стало быть, таким же индуктивным поведением во всём практически важном диапазоне частот.

Ранее²⁾ аналогичный радиус был найден для ёмкости семипроволочной жилы. Причём его величина численно совпадает с индуктивным. Видимо, это связано с теоремой об обратном отношении межпроводных ёмкостей и индуктивностей.

Выводы
1. Погрешность расчётов индуктивных параметров ~ 0.1..0.3% в программной среде ELCUT не превышает погрешность ёмкостных.
2. Межпроводная индуктивность L и индуктивные параметры Lж не осесимметричных жил не имеют однозначного определения. Однако, однозначно определён инвариантный индуктивный параметр L + Lж .
3. Многопроволочную жилу (и вообще произвольной формы) можно заменить круглым проводом с некоторым эффективным радиусом, который для наиболее характерных форм кабельных жил и их окружения можно вычислить раз и навсегда.

Конформное отображение уравнений Лапласа и Пуассона

Функция w(z) = u + j v где z = x + jy, а u (х,у) и v(x,y) удовлетворяют условиям

∂u/ ∂ x = ∂v / ∂y; ∂u / ∂y = – ∂v / ∂x или u_x = v_y; u_y = –v_x

реализует конформное преобразование фигур (образов) из плоскости х, у в их отображения в плоскости u, v. А функции х(u,v) и у(u,v) – обратное отображение.

В операторе Лапласа это просто замена переменных:

∂U = U_xx + U_yy = D (U_uu + U_vv)

где определитель

D = ∂(u,v) / ∂(x,y) = u_xv_y – u_yv_x

Таким образом, конформное преобразование не меняет вид уравнения Лапласа:

U_xx + U_yy = 0 => U_uu + U_vv = 0

Но, вообще говоря, меняет вид уравнения Пуассона. Во всяком случае, его правой части. Например, для потенциала U электрического поля

U_xx + U_yy = – ρ (х, у) /εε₀   (*)

где = ρ (х, у) и ρ (u,v) – плотность заряда.

Она имеет смысл производной ρ = dQ / dS, где Q (x,y) – функция распределения заряда по поверхности, а dS = dxdy – элемент площади. При замене переменных элемент площади трансформируется

dS’ = dudv = (∂(u,v) / ∂(x,y))1/2 dxdy = √|D| dxdy

Подставим это в (*):

D (Uuu + Uvv) = – dQ(х(u,v), у(u,v))/(εε₀ dudv/√|D|)

И получаем уравнение Пуассона в переменных u, v ΔU(u,v) = – ρ (х, у) / εε₀, где ρ(u,v) = dQ(х(u,v), у(u,v)) / (dudv √|D|) = ρ(х(u,v), у(u,v)) / √|D|

Таким образом, чтобы получить «новую» плотность заряда, надо в «старой» заменить х,у на u,v, и разделить на √|D|. Отметим, что если в правой части уравнения Пуассона не плотность зарядов, а,скажем, точечный заряд, то его надо разделить на D.

Более того, дробно-линейное конформное отображение сохраняет вид не только уравнения Лалпаса, но и Пуассона.

Доказательство

Пусть в плоскости x,y действует дробно-линейное отображение w = M²/z .

Тогда u = M²x / r² и v = – M²y / r² и обратно: x = M²u / R² и y = – M²v / R²,

где: r² = x² + y²; R² = u² + v² = M⁴/r².

В этом случае D = (∂(R,φ) / ∂(r,φ)) = – M²/r². А уравнение Пуассона (в полярных координатах):

U_rr + U_r/r + U_φφ /r² = – ρ(r,φ)/εε₀; U_RR + U_R/R + U_φφ/R² = – ρ(M²/R, φ) M2/(R²εε₀)

Аналогично для вектор-потенциала магнитного поля

A_rr + A_r/r + A_φφ /r² = – δ(r, φ)/εε₀; A_RR + AR/R + A_φφ/R²2 = – δ(M²/R, φ) M²/(R²εε₀), где δ – плотность тока.

Видно, что все уравнения отличаются только обозначением переменных. Что и требовалось доказать.

Индуктивный инвариант

Исходим из телеграфного уравнения

– (∂/∂t) ∫ В(r) dr = Uz + Еэ + Еж (**)

где: Еэ = δэ / σэ, Еж = δж/σж. Запишем в алгебраической форме

– jωLJ = Uz – Re(δэ) / σэ – j Im(δэ) / σэ – Re(δж) / σж – j Im(δж) / σж

– jωJ (L – Im(δж) / Jωσж – Im(δэ) / Jωσэ) = Uz – Re(δэ) / σэ – Re(δж) / σж)

по определению Im(δж) / Jδσж = – Lж, Im(δэ ) / Jωσ = – Lэ.

Поэтому

– jωJ (L + Lж + Lэ) = Uz – Re(δэ) / σэ – Re(δж) / σж

Правая часть зависит от (градиента) потенциала сечения плоскостью z поверхности проводов. В приближении телеграфных уравнений это сечение – линия равного потенциала и его градиентов. Следовательно, правая часть не зависит от положения точек на указанной линии. Следовательно, такой же инвариант и величина L + Lж + Lэ. Если один из проводников, например, экран – сверхпроводящий, то Lэ = 0 и инвариант вырождается в L + Lж. Что и требовалось доказать.

¹⁾ Вишняков Е.М., Хвостов Д.В. Расчёт межпроводниковой индуктивности и ёмкости симметричных прямых пар методами конформных отображений и конечных элементов. Кабель №3, 2007.
²⁾ Вишняков Е.М., Хвостов Д.В. Влияние скрутки на межпроводниковую ёмкость витых пар и триад. Кабель №4, 2007.
³⁾ П.Л.Калантаров, Л.А.Цейтлин. Расчёт индуктивностей. – Л:Энергоатомиздат, 1986, стр. 94.
⁴⁾ Л.А.Бессонов. Теоретические основы электротехники.– М: ВШ, 1967